Virtual Prototyping of a Dual-Mode Circular Waveguide Filter
A Circular-Waveguide Dual-Mode Filter
Circular-waveguide dual-mode (CWDM) filters are key in communication satellite output multiplexers, praised for their high-Quality Factor (Q) and narrow bandwidth band-pass filtering. Research focuses on their electromagnetic (EM) modeling and design, highlighting their dual-mode resonance with a single resonator. This makes CWDM filters crucial for advancing satellite communication technologies.
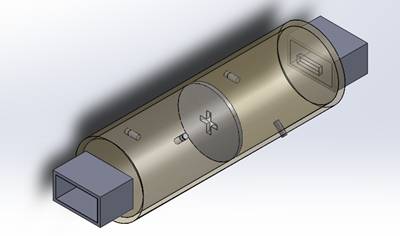
Figure 1 - Circular-Waveguide Dual-Mode Filter
Dimensions
The figure below offers comprehensive views of the filter's model, with all key dimensions meticulously annotated for clarity.
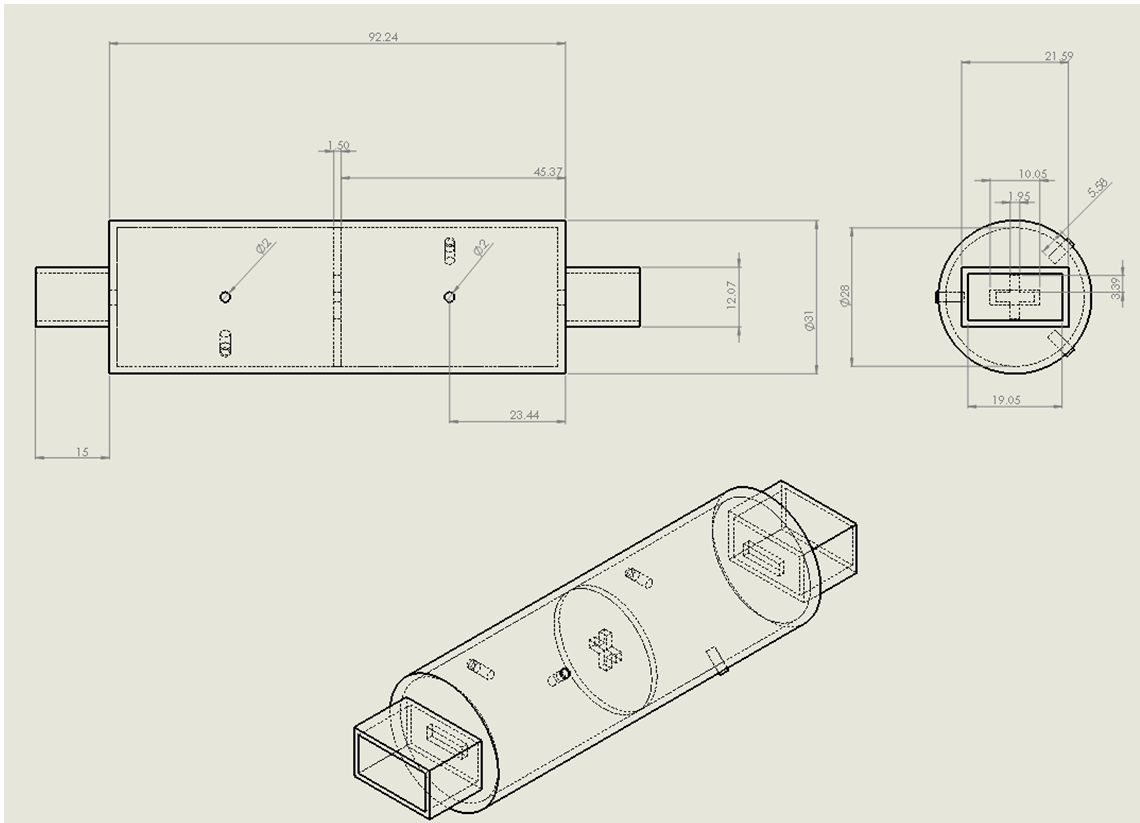
Simulation
The model has been finely tuned for optimal performance, showcasing enhanced efficiency and precise matching at 11 GHz for Ku Band communications. Utilizing a scattering parameter solver, it offers two frequency plans: Fast Sweep for quick results and Discrete Sweep for higher accuracy away from the center frequency. Special attention has been given to the Finite Element mesh, especially around the screws, with finer mesh control for greater detail and accuracy in these crucial areas.
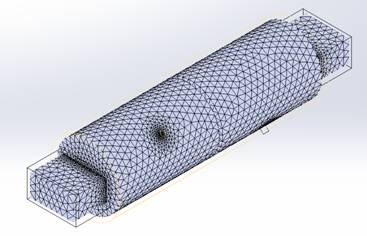
Figure 2 - Filter's surface mesh
Load/ Restraint
The hollow parallelepiped's lateral faces serve as the waveguide's input and output. The circular filter's extruded boss's outer face is treated as a perfect electric conductor (PEC). Air fills the hollow interior, while the internal shapes are also designated as PECs.
Results
The output results indicate excellent performance, confirming the filter's suitability for its intended application domain.
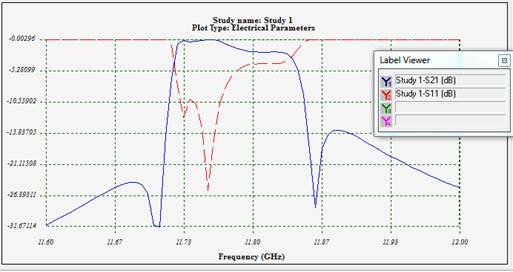
Figure 3 - Insertion and return loss of the filter
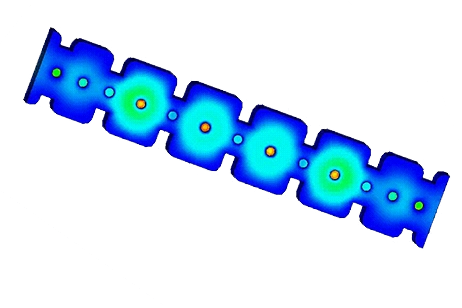
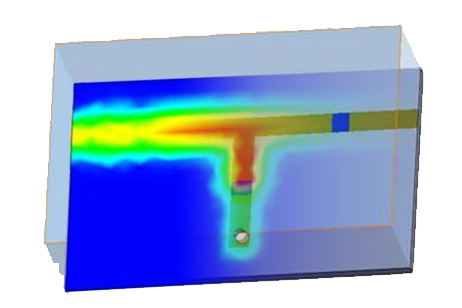
By leveraging HFWorks' 3D viewer and the section clipping feature, we gain an insightful perspective into the circular waveguide's interior, enabling us to observe the electric field distribution over time. This visualization captures the wave's propagation from the input to the output.
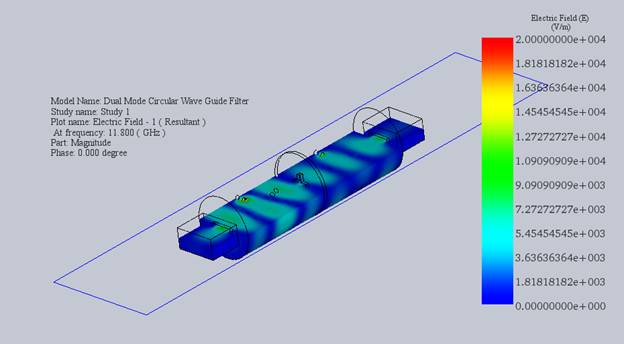
Figure 4 - Inner distribution of electric field at 11.8 GHz
Conclusion
The Circular-Waveguide Dual-Mode Filter (CWDM) stands out as a critical component in communication satellite output multiplexers, boasting high-quality Factor (Q) and narrow bandwidth band-pass filtering. This research delves into the electromagnetic (EM) modeling and design of CWDM filters, emphasizing their resonance with a single resonator, which is pivotal for advancing satellite communication technologies.
Simulation techniques, particularly utilizing HFWorks, were pivotal in refining the model for optimal performance, achieving precise matching at 11 GHz for Ku Band communications. The results showcase exceptional performance, affirming the filter's suitability for its intended application domain. Leveraging HFWorks' visualization tools provides valuable insights into the filter's internal workings, enabling a detailed examination of the electric field distribution over time. This comprehensive analysis underscores the significance of CWDM filters in modern communication systems, particularly in satellite technology.
References
[1] An Optimal Circular-Waveguide Dual-Mode Filter Without Tuning Screws Ke-Li Wu, Senior Member, IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES, VOL. 47, NO. 3, MARCH 1999