How Does the Halbach Array Improve Magnetic Levitation?
Magnetic Levitation
Maglev, employing magnetic fields, suspends objects without contact, countering gravity and accelerations. It's vital in maglev trains, melting, bearings, and displays. By combining permanent magnets, electromagnets, and superconductors, successful levitation and 6-axis control are achieved. However, planar actuators lack the required accuracy due to challenging magnetic force and deflection modeling. This example focuses on a planar magnetic actuator with a Halbach array on an aluminum plate, aiming to compute magnetic forces on the plate accurately.
Multiphysics simulation
EMS seamlessly couples magnetic field and structural analyses. When an array of permanent magnets is mounted on a mechanical structure, the magnetic fields and forces induce deformations in the structure.

Figure 1 - Planar actuator mounted on an aluminum carrier
CAD Model
The magneto-structural system under analysis comprises a Halbach array (11x11) affixed to a conductive aluminum plate, as depicted in Figure 2. The primary objective of this example is to assess the deflection of the plate. All dimensions are provided in millimeters.
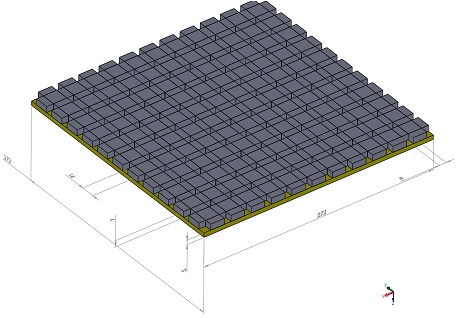
Figure 2 - The planar actuator model
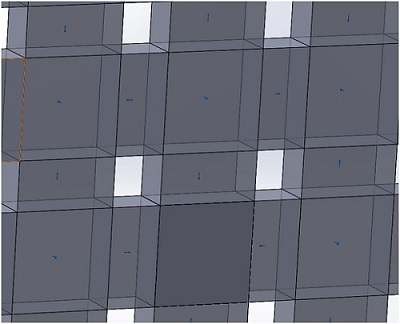
Figure 3 - Coercivity direction (in blue arrows) of the magnets forming the Halbach array
Material properties
| Permeability | Coercivity (A/m) | Remanence(T) | |
| NdFeB | 1.04 | 948808.3 | 1.24 |
Meshing
The high-quality mesh ensures accurate results. EMS provides flexible mesh control tools, allowing refinement on faces, edges, and bodies. In this model, a refined mesh is applied to the aluminum plate and magnet array for precise magnetic force calculations. Mechanical stress analysis relies on accurate magnetic results. Figure 4 displays the mesh used for the current analysis.

Figure 4 -The meshed model
Magneto-structural Results
-
Magnetic flux density plot
Figure 5 illustrates the magnetic flux density plot generated by the magnets in the analyzed planar actuator.
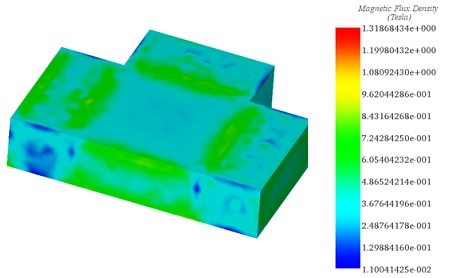
Figure 5 - 3D fringe plot of the magnetic flux density in the model
- Magnetic force density plot
Figure 6 below depicts a fringe plot showcasing the magnetic force density. Maximum force values occur at the boundaries of the magnets, particularly where they face each other.
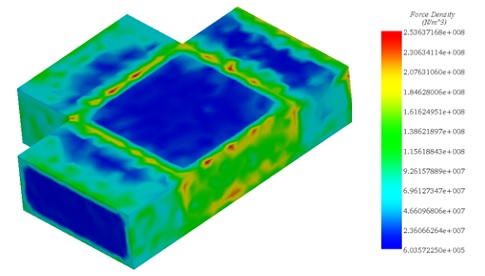
Figure 6 - Magnetic force density plot
- Displacement along the Z axis of the plate
Under the influence of magnetic forces, the plate bends toward its center, exhibiting significant deflection. EMS results align closely with experimental and numerical findings provided in [1].
| EMS Result | The reference result | |
| Deflection of the plate along Z axis (in m) | 1.8e-04 | 2e-04 |
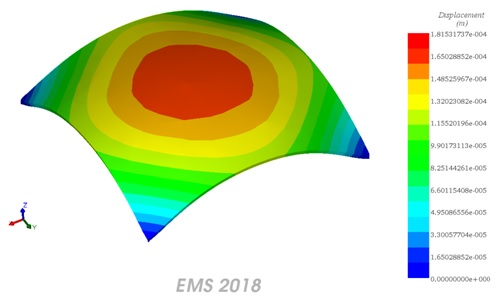
Figure 7 - Displacement along the Z axis of the plate (the deformed shape)
Conclusion
This application note explores the capabilities of magnetic levitation (Maglev) technology, particularly focusing on a planar magnetic actuator equipped with a Halbach array to levitate an aluminum plate. Maglev technology, which employs magnetic fields to suspend objects without any contact, thereby overcoming gravity and other accelerations, is crucial in various applications such as maglev trains, melting processes, bearings, and display systems. The primary challenge in planar actuators like the one studied is achieving the required accuracy in magnetic force and deflection modeling to ensure precise control and levitation.
The multiphysics simulation conducted with EMS combines magnetic field and structural analyses to assess the induced deformations on the aluminum plate by the magnetic fields generated by a Halbach array of permanent magnets. This comprehensive analysis aims to accurately compute the magnetic forces acting on the plate and predict its deflection. The use of a refined mesh on the aluminum plate and magnet array enables precise calculations of magnetic forces and the subsequent mechanical stress analysis.
Results from the simulation show significant deflection of the aluminum plate towards its center, underlining the effectiveness of the magnetic actuator design. The comparison between EMS results and reference data demonstrates a close alignment, validating the simulation's accuracy in predicting the behavior of maglev systems.
References
[1] J. M. M. Rovers, J. W. Jansen, E. A. Lomonova and M.J.C. Ronde . Calculation of the static forces among the permanents magnets in a Halbach Array. IEEE Transactions on Magnetics, Volume 45,NO 10. October 2009: Netherlands.?